ਹਿਸਾਬ ਦਾ ਡਰ ਸੰਸਾਰ ਵਿਆਪਿਕ ਹੈ। ਆਪਣੇ ਤਿੰਨ ਦਹਾਕਿਆਂ ਦੇ ਕੋਚਿੰਗ ਕਲਾਸਾਂ  ਦੇ ਅਨੁਭਵ ਦੌਰਾਨ ਮੈਂ ਵੇਖਿਆ ਹੈ ਕਿ ਕੁੱਲ ਮਿਲਾ ਕੇ ਹਿਸਾਬ ਦੇ ਵਿਦਿਆਰਥੀ ਦੋ ਕਿਸਮ ਦੇ ਹੁੰਦੇ ਹਨ। ਪਹਿਲੇ ਉਹ ਜੋ ਹਿਸਾਬ ਵਿੱਚ ਬਹੁਤ ਹੁਸ਼ਿਆਰ ਹੁੰਦੇ ਹਨ, ਹੋ ਸਕਦਾ ਹੈ ਕਿ ਉਹ ‘ਗੌਡ ਗਿਫਟਡ’ ਹੋਣ ਜਾਂ ਫਿਰ ਸਖਤ ਮਿਹਨਤੀ ਪਰ ਉਹ ਅਸਲ ਵਿੱਚ ਹੀ ਹਿਸਾਬ ਦੀ ਢੂੰਗੀ ਸਮਝ ਰਖਦੇ ਹਨ। ਦੂਸਰੇ ਉਹ ਵਿਦਿਆਰਥੀ ਜਿਹੜੇ ਹਿਸਾਬ ਵਿੱਚ ਬਹੁਤ ਕਮਜੋਰ ਹੁੰਦੇ ਹਨ ਅਤੇ ਉਨ੍ਹਾਂ ਨੂੰ ਪੱਕਾ ਵਿਸ਼ਵਾਸ ਹੁੰਦਾ ਹੈ ਕਿ ਹਿਸਾਬ ਦਾ ਵਿਸ਼ਾ ਉਨ੍ਹਾਂ ਦੇ ਵੱਸ ਦੀ ਗੱਲ ਨਹੀਂ। ਉਨ੍ਹਾਂ ਅੰਦਰ ਹਿਸਾਬ ਦਾ ਇਹ ਡਰ ਪੂਰੀ ਤਰਾਂ ਹਾਵੀ ਹੋ ਚੁੱਕਾ ਹੁੰਦਾ ਹੈ। ਇੰਨ੍ਹਾਂ ਵਿਚੋਂ ਕੁਝ ਨੇ ਹੋ ਸਕਦਾ ਹੈ ਕਿ ਆਪਣੇ ਸਕੂਲ ਦੇ ਦਿਨਾਂ ਇਸ ਡਰ ਤੋਂ ਛੁਟਕਾਰੇ ਲਈ ਗੰਭੀਰ ਕੋਸ਼ਿਸ਼ਾਂ ਕੀਤੀਆਂ ਹੋਣ ਪ੍ਰੰਤੂ ਉਹ ਇਸ ਵਿਸ਼ੇ ਨੂੰ ਸਮਝ ਨਹੀਂ ਪਾਏ। ਇਸ ਸਭ ਦਾ ਕਾਰਨ ਕੁਝ ਵੀ ਹੋ ਸਕਦਾ ਹੈ ਪ੍ਰੰਤੂ ਪ੍ਰਮਾਤਮਾਂ ਦਾ ਸ਼ਰਾਪ ਕਦੇ ਵੀ ਨਹੀਂ ਹੋ ਸਕਦਾ (ਜਿਵੇਂ ਕਿ ਕੁਝ ਲੋਕ ਦਲੀਲ ਦਿੰਦੇ ਹਨ) । ਦੂਸਰੇ ਪਾਸੇ ਇੰਨ੍ਹਾਂ ਵਿਦਿਆਰਥੀਆਂ ਦੇ ਮਨਾਂ ਵਿਚੋਂ ਹਿਸਾਬ ਦਾ ਡਰ ਕੱਢ ਕੇ ਅਤੇ ਵਿਸ਼ਵਾਸ ਭਰ ਕੇ ਅਤੇ ਇਸ ਨੂੰ ਇੱਕ ਖੇਡ ਬਣਾ ਕੇ ਹਿਸਾਬ ਵਿੱਚ ਹੁਸ਼ਿਆਰ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ।

ਹਿਸਾਬ ਵਿੱਚ ਹੁਸ਼ਿਆਰ ਬਨਣ ਲਈ ਪਹਿਲੀ ਜ਼ਰੂਰਤ ਹਿਸਾਬ ਪੜ੍ਹ ਸਕਣ ਦਾ ਵਿਸ਼ਵਾਸ ਹੈ। ਬਹੁਤ ਸਾਰੇ ਮਾਮਲਿਆਂ ਵਿੱਚ ਇਸ ਵਿਸ਼ਵਾਸ ਦੀ ਘਾਟ ਹੀ ਵਿਦਿਆਰਥੀ ਦੇ ਹਿਸਾਬ ਵਿੱਚ ਕਮਜੋਰ ਹੋਣ ਹੋਣ ਦਾ ਕਾਰਨ ਬਣਦੀ ਹੈ। ਸੀਨੀਅਰ ਕਲਾਸਾਂ ਖਾਸ ਕਰਕੇ 8ਵੀਂ ਜਮਾਤ ਦੇ ਬਾਦ, ਹਿਸਾਬ ਦੇ ਕਮਜ਼ੋਰ ਵਿਦਿਆਰਥੀ ਲਈ ਹੁਸ਼ਿਆਰ ਬਨਣਾ ਅਸਲ ਵਿੱਚ ਹੀ ਮੁਸ਼ਕਿਲ ਹੁੰਦਾ ਹੈ। ਫਿਰ ਵੀ ਮੈਂ ਵਿਸ਼ਵਾਸ ਕਰਦਾ ਹਾਂ ਕਿ ‘ਕੁਝ ਵੀ ਚੰਗਾ ਸ਼ੁਰੂ ਕਰਨ ਲਈ ਕਦੇ ਵੀ ਦੇਰ ਨਹੀਂ ਹੁੰਦੀ’ ਅਤੇ ‘ਕੁਝ ਵੀ ਕਰਨਾਂ ਅਸੰਭਵ ਨਹੀਂ, ਬਸ ਅਸੀਂ ਵਿਸ਼ਵਾਸ ਕਰੀਏ ਕਿ ਇਹ ਸੰਭਵ ਹੈ’।

ਮੈਂ ਇੱਥੇ ਹਿਸਾਬ ਦੇ ਕੁਝ ‘ਸ਼ਾਰਟਕੱਟ’ (ਸਰਲ ਤਰੀਕੇ) ਦਾ ਵਰਨਣ ਕਰਨ ਜਾ ਰਿਹਾ ਹਾਂ ਜਿਸ ਰਾਹੀਂ ਹਿਸਾਬ ਨੂੰ ਇੱਕ ਖੇਡ ਬਣਾਇਆ ਜਾ ਸਕਦਾ ਹੈ, ਪਰੰਤੂ ਇਹ ਕੇਵਲ ਉਨ੍ਹਾਂ ਲਈ ਸੰਭਵ ਹੈ ਜੋ ਇਨ੍ਹਾਂ ਦਾ ਅਭਿਆਸ ਕਰਦੇ ਹਨ, ਕੇਵਲ ਪੜ੍ਹ ਲੈਣ ਨਾਲ ਕੋਈ ਲਾਭ ਨਹੀਂ ਹੋਣ ਵਾਲਾ।

ਇੱਕ ਅਜਿਹਾ ਖੇਤਰ ਜਿਹੜਾ ਆਮ ਕਰਕੇ ਛੋਟੇ ਵੱਡੇ ਹਰ ਤਰਾਂ ਦੇ ਵਿਦਿਆਰਥੀਆਂ ਨੂੰ ਤੰਗ ਕਰਦਾ ਹੈ, ਉਹ ‘ਫਰੈਕਸ਼ਨ’, ‘ਖੰਡ’ ਜਾਂ ਭਿੰਨ ਹੈ। ਇਸ ਵਿਸ਼ੇ ਤੇ ਕੁਝ ਸਾਧਾਰਨ ਜਿਹੀਆਂ ਸੱਚਾਈਆਂ ਦਾ ਜ਼ਿਕਰ ਕਰਨਾਂ ਚਾਹਾਂਗਾ। ਜੇਕਰ ਦੋ ਜਾਂ ਦੋ ਤੋਂ ਵੱਧ ਭਿੰਨਾਂ ਨੂੰ ਜੋੜਣਾ ਹੋਵੇ ਜਾਂ ਘਟਾਉਣਾ ਹੋਵੇ ਤਾਂ ‘ਮਿਕਸ ਫਰੈਕਸ਼ਨ’ ਨੂੰ ਪਹਿਲਾਂ ‘ਇੰਮਪਰਾਪਰ ਫਰੈਕਸ਼ਨ’ ਵਿੱਚ ਬਦਲਣਾ ਪੈਂਦਾ ਹੈ। ਫਿਰ ਹਰ (ਡਿਨਾਮੀਨੇਟਰ) ਦਾ ਲਘੁਤਮ ਸਮਾਵਰਤਕ (ਐਲਸੀਐਮ) ਲੈ ਕੇ ਫਿਰ ਕਈ ਤਰਾਂ ਦੀ ਗੁਣਾ, ਭਾਗ, ਜੋੜ ਅਤੇ ਘਟਾਓ ਕਰ ਕੇ ਸਵਾਲ ਹੱਲ ਕੀਤਾ ਜਾਂਦਾ ਹੈ। ਘੱਟ ਤੋਂ ਘੱਟ ਦੋ ਭਿੰਨਾਂ ਲਈ ਤਾਂ ਅਜਿਹੇ ਲੰਬੇ ਰਸਤੇ ਦੀ ਕੋਈ ਲੋੜ ਨਹੀਂ। ਭਿੰਨ ਛੋਟੀ ਹੋਵੇ ਜਾਂ ਵੱਡੀ ‘ਇੰਮਪਰਾਪਰ’ ਵਿੱਚ ਬਦਲਣ ਦੀ ਕੋਈ ਲੋੜ ਨਹੀਂ। ਪੂਰਣ (ਹੋਲ) ਅੰਕਾ ਨੂੰ ਜੋੜਣ ਤੋਂ ਬਾਦ ਭਿੰਨਾਂ ਨੂੰ ਵੱਖ ਤੋਂ ਜੋੜਿਆ ਜਾ ਸਕਦਾ ਹੈ।

ਇਥੇ ਅਸੀਂ 2 ਅਤੇ 11 ਨੂੰ ਜੋੜ ਕੇ 13 ਪ੍ਰਾਪਤ ਕਰਦੇ ਹਾਂ ਅਤੇ ‘ਕਰਾਸ ਮਲਟੀਪਲਾਈ’ ਕਰਕੇ 3 x 1 = 3 ਅਤੇ 2 x 7 = 14, ਅਤੇ ਜੋੜ ਕਰਕੇ 3 + 14 = 17, ‘ਡਿਨਾਮੀਨੇਟਰ’ ਨੂੰ ਗੁਣਾ ਕਰਕੇ 3 x 7 = 21,
 

ਉੱਤਰ ਆਵੇਗਾ:

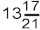ਜੇਕਰ 2 ਦੀ ਥਾਂ ਤੇ 345 ਹੁੰਦਾ ਜਾਂ 11 ਦੀ ਥਾਂ 678 ਵੀ ਹੁੰਦਾ ਤਾਂ ਸਾਡਾ ਤਰੀਕਾ ਫਿਰ ਵੀ ਉਹ ਹੀ ਰਹਿੰਦਾ। ਅਸੀਂ ਪਹਿਲਾਂ 345 ਅਤੇ 678 ਨੂੰ ਜੋੜਦੇ ਤੇ ਫਿਰ ਭਿੰਨਾਂ ਨੂੰ। ਇਸ ਤਰਾਂ ਅਸੀਂ 95% ਤੱਕ ਸਮਾਂ ਬਚਾ ਸਕਦੇ ਸੀ। ਭਿੰਨਾਂ ਦੇ ਘਟਾਓ ਦੇ ਸਵਾਲ ਵੀ ਇਸੇ ਤਰੀਕੇ ਨਾਲ ਹੱਲ ਕੀਤੇ ਜਾ ਸਕਦੇ ਹਨ। ਦੋ ਤੋਂ ਵੱਧ ਰਕਮਾਂ ਦੇ ਜੋੜ, ਘਟਾਓ, ਜੋੜ ਅਤੇ ਘਟਾਓ ਅਤੇ ਗੁਣਾ ਜਾਂ ਭਾਗ ਤੱਕ ਦੇ ਸਵਾਲ ਵੀ ‘ਮਿਕਸ ਫਰੈਕਸ਼ਨ’ ਨੂੰ ‘ਇੰਮਪਰਾਪਰ’ ਵਿੱਚ ਬਦਲੇ ਤੋਂ ਬਿਨਾਂ ਹੱਲ ਕੀਤੇ ਜਾ ਸਕਦੇ ਹਨ। ਇਸ ਤਰੀਕੇ ਨਾਲ ਬੱਚਿਆਂ ਵਿੱਚ ਹਿਸਾਬ ਪ੍ਰਤੀ ਡਰ ਦੂਰ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ ਅਤੇ ਵਿਸ਼ੇ ਦੀ ਬੇਹਤਰ ਸਮਝ ਪੈਦਾ ਕੀਤੀ ਜਾ ਸਕਦੀ ਹੈ।

ਇਸੇ ਤਰਾਂ ਅੱਧੇ ਜਾਂ ਚੌਥੇ (ਭਿੰਨ) ਦਾ ਵਰਗ ਪਤਾ ਕਰਨਾ ਵੀ ਬਿਲਕੁਲ ਸੌਖਾ ਹੈ। ਅੱਧੇ ਵਾਲੀਆਂ ਭਿੰਨਾਂ ਦਾ ਵਰਗ ਪਤਾ ਕਰਨ ਲਈ ਪੂਰਣ (ਹੋਲ) ਅੰਕ ਨੂੰ ਅਗਲੇ (+1) ਨਾਲ ਗੁਣਾ ਕਰੋ ਅਤੇ ਅੰਤ ਵਿੱਚ ¼ ਲਿਖੋ। ਉੱਤਰ ਹਾਜ਼ਰ ਹੈ

ਚੌਥੇ ਹਿੱਸੇ ਵਾਲੀਆਂ ਭਿੰਨਾਂ ਦਾ ਵਰਗ ਪਤਾ ਕਰਨ ਲਈ ਪੂਰਣ (ਹੋਲ) ਅੰਕ ਦਾ ਵਰਗ ਕਰੋ ਅਤੇ ਇਸ ਅੰਕ ਦਾ ਅੱਧ ਇਸ ਵਿੱਚ ਜੋੜ ਦਿਓ, ਫਿਰ ਅੰਤ ਵਿੱਚ 1/16 ਲਾ ਦਿਓ। ਜੇਕਰ ਪੂਰਣ ਅੰਕ ‘ਔਡ’ (ਟਾਂਕ) ਹੋਵੇ ਤਾਂ ਫਿਰ ਅੰਤ ਵਿੱਚ 9/16 ਆਵੇਗਾ।

8¼ X 8¼ = (8 X 8 +8/2) 1/16   = (64 + 4) 1/16   = 68⅟16

4¼ X 4¼ = 18⅟16                ਉੱਤਰ ਹਾਜ਼ਰ ਹੈ

ਮੈਂ ਇੱਕ ਘਟਨਾ ਦਾ ਜ਼ਿਕਰ ਇੱਥੇ ਜ਼ਰੂਰ ਕਰਨਾ ਚਾਹਾਂਗਾ। ਮੈਂ ਮੇਜਰ ਅਜਾਇਬ ਸਿੰਘ ਸੀਨੀਅਰ ਸੈਕੰਡਰੀ ਸਕੂਲ, ਜੀਵਣ ਵਾਲਾ ਵਿਖੇ ਸਮਰਕੈਂਪ ਵਿੱਚ ਕਿਉਮੈਥਸ ਦੀ ਕਲਾਸ ਲੈ ਰਿਹਾ ਸੀ। ਮੈਨੂੰ ਇੱਕ ਵਿਦਿਆਰਥੀ ਨੇ ਸਵਾਲ ਕੀਤਾ ਕਿ ਕੀ ਮੈਨੂੰ 61 ਦਾ ਪਹਾੜਾ (ਟੇਬਲ) ਆਉਂਦਾ ਹੈ? ਮੇਰਾ ਜਵਾਬ ਸੀ ਕਿ ਕੁਝ ਸਮੇ ਬਾਦ ਇੱਥੇ ਬੈਠੇ ਸਾਰੇ ਵਿਦਿਆਰਥੀਆਂ ਨੂੰ 61 ਦਾ ਪਹਾੜਾ ਆਉਂਦਾ ਹੋਵੇਗਾ। ਮੈਂ 6 ਦੇ ਟੇਬਲ ਨੂੰ ਉਰਦੂ ਵਾਂਗ ਲਿਖ ਕੇ ਬੱਚਿਆਂ ਨੂੰ ਦੱਸਿਆ। ਅਸਲ ਵਿੱਚ ਇਹ ਸਭ ਕੁਝ ਬੱਚਿਆਂ ਵਿੱਚ ਹਿਸਾਬ ਪ੍ਰਤੀ ਦਿਲਚਸਪੀ ਪੈਦਾ ਕਰਨ ਲਈ ਕੀਤਾ ਗਿਆ ਸੀ।

ਉਰਦੂ ਵਾਂਗ ਸੱਜੇ ਤੋਂ ਖੱਬੇ ਵੱਲ ਲਿਖੋ:

61	6		1
122	12		2
183	18		3
244	24		4
305	30		5
366	36		6
427	42		7
488	48		8
549	54		9
610	61		0

ਅਸੀਂ 1 ਨਾਲ ਖਤਮ ਹੋਣ ਵਾਲੇ ਕਿਸੇ ਵੀ ਅੰਕ ਦਾ ਟੇਬਲ (ਪਹਾੜਾ) ਇਸੇ ਤਰੀਕੇ ਨਾਲ ਲਿਖ ਸਕਦੇ ਹਾਂ। ਜੇਕਰ ਕੋਈ ਅਧਿਆਪਕ ਇਸ ਤਰਾਂ ਟੇਬਲ ਲਿਖਣਾ ਦੱਸਣ ਦੇ ਨਾਲ ਅਜਿਹਾ ਹੋਣ ਦੇ ਕਾਰਣਾ ਨੂੰ ਵੀ ਦੱਸਦਾ ਹੈ ਤਾਂ ਵਿਦਿਆਰਥੀ ਨੂੰ ਗੁਣਾ ਦੇ ਮਾਮਲੇ ਵਿੱਚ ਵਧੇਰੇ ਸਮਝ ਆ ਸਕਦੀ ਹੈ। ਅਜਿਹਾ ਕਰਨ ਨਾਲ ਵਿਦਿਆਰਥੀਆਂ ਵਿੱਚ ਹਿਸਾਬ ਪ੍ਰਤੀ ਸਵੈ ਭਰੋਸਾ ਪੈਦਾ ਹੁੰਦਾ ਹੈ। ਇੱਕ ਵਿਦਿਆਰਥੀ ਨੂੰ ਜਦੋਂ ਅਜਿਹਾ ਦੱਸਿਆ ਗਿਆ ਤਾਂ ਘਰ ਜਾ ਕੇ ਉਸਨੇ ਆਪਣੇ ਚਾਚੇ ਨੂੰ ਸਵਾਲ ਕੀਤਾ ਕਿ ਕੀ ਉਹ 201 ਦਾ ਟੇਬਲ ਲਿਖ ਸਕਦਾ ਹੈ। ਬੱਚੇ ਵਿੱਚ ਪੈਦਾ ਹੋਈ ਹਿਸਾਬ ਬਾਰੇ ਦਿਲਚਸਪੀ ਦਾ ਤੁਸੀਂ ਖੁਦ ਅੰਦਾਜਾ ਲਗਾ ਸਕਦੇ ਹੋ।

...........ਬਾਕੀ ਅਗਲੇ ਲੇਖਾਂ ਵਿੱਚ।